One to One Functions - Graph, Examples | Horizontal Line Test
What is a One to One Function?
A one-to-one function is a mathematical function whereby each input correlates to just one output. So, for each x, there is a single y and vice versa. This signifies that the graph of a one-to-one function will never intersect.
The input value in a one-to-one function is known as the domain of the function, and the output value is noted as the range of the function.
Let's study the examples below:
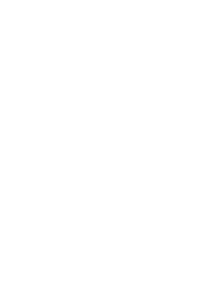
For f(x), any value in the left circle corresponds to a unique value in the right circle. In conjunction, each value on the right corresponds to a unique value in the left circle. In mathematical words, this implies every domain has a unique range, and every range owns a unique domain. Hence, this is an example of a one-to-one function.
Here are some different examples of one-to-one functions:
-
f(x) = x + 1
-
f(x) = 2x
Now let's examine the second example, which displays the values for g(x).
Be aware of the fact that the inputs in the left circle (domain) do not hold unique outputs in the right circle (range). Case in point, the inputs -2 and 2 have the same output, i.e., 4. In the same manner, the inputs -4 and 4 have the same output, i.e., 16. We can see that there are matching Y values for numerous X values. Hence, this is not a one-to-one function.
Here are different representations of non one-to-one functions:
-
f(x) = x^2
-
f(x)=(x+2)^2
What are the characteristics of One to One Functions?
One-to-one functions have the following qualities:
-
The function owns an inverse.
-
The graph of the function is a line that does not intersect itself.
-
The function passes the horizontal line test.
-
The graph of a function and its inverse are equivalent regarding the line y = x.
How to Graph a One to One Function
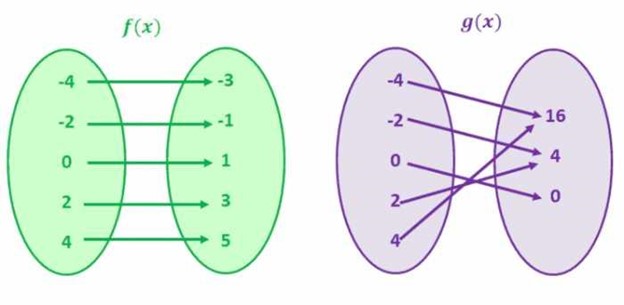
In order to graph a one-to-one function, you will have to determine the domain and range for the function. Let's look at a straight-forward example of a function f(x) = x + 1.
Once you have the domain and the range for the function, you need to plot the domain values on the X-axis and range values on the Y-axis.
How can you evaluate whether a Function is One to One?
To indicate if a function is one-to-one, we can leverage the horizontal line test. As soon as you plot the graph of a function, trace horizontal lines over the graph. If a horizontal line moves through the graph of the function at more than one place, then the function is not one-to-one.
Due to the fact that the graph of every linear function is a straight line, and a horizontal line will not intersect the graph at more than one spot, we can also conclude all linear functions are one-to-one functions. Keep in mind that we do not use the vertical line test for one-to-one functions.
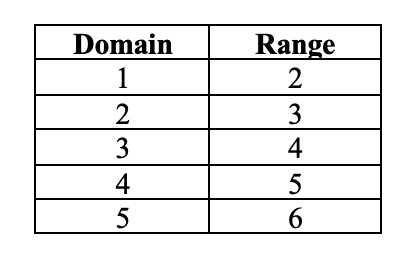
Let's study the graph for f(x) = x + 1. Once you plot the values for the x-coordinates and y-coordinates, you have to consider whether a horizontal line intersects the graph at more than one place. In this instance, the graph does not intersect any horizontal line more than once. This signifies that the function is a one-to-one function.
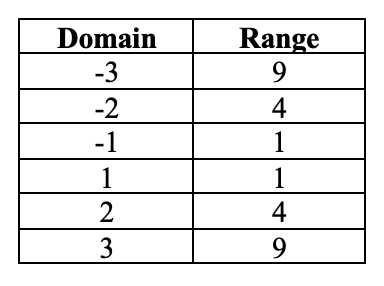
On the contrary, if the function is not a one-to-one function, it will intersect the same horizontal line more than one time. Let's examine the graph for the f(y) = y^2. Here are the domain and the range values for the function:
Here is the graph for the function:
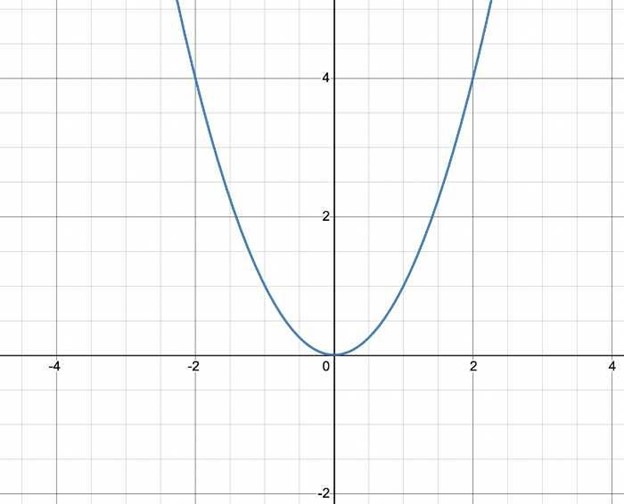
In this example, the graph crosses multiple horizontal lines. For example, for either domains -1 and 1, the range is 1. In the same manner, for each -2 and 2, the range is 4. This signifies that f(x) = x^2 is not a one-to-one function.
What is the inverse of a One-to-One Function?
Since a one-to-one function has only one input value for each output value, the inverse of a one-to-one function is also a one-to-one function. The inverse of the function basically reverses the function.
For Instance, in the event of f(x) = x + 1, we add 1 to each value of x for the purpose of getting the output, or y. The inverse of this function will deduct 1 from each value of y.
The inverse of the function is f−1.
What are the qualities of the inverse of a One to One Function?
The qualities of an inverse one-to-one function are the same as any other one-to-one functions. This signifies that the reverse of a one-to-one function will hold one domain for each range and pass the horizontal line test.
How do you determine the inverse of a One-to-One Function?
Finding the inverse of a function is simple. You simply need to swap the x and y values. Case in point, the inverse of the function f(x) = x + 5 is f-1(x) = x - 5.
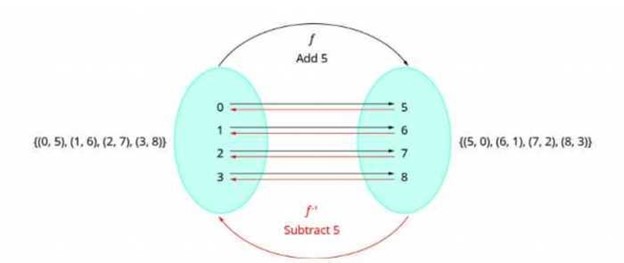
As we reviewed before, the inverse of a one-to-one function reverses the function. Because the original output value required adding 5 to each input value, the new output value will require us to deduct 5 from each input value.
One to One Function Practice Questions
Examine the subsequent functions:
-
f(x) = x + 1
-
f(x) = 2x
-
f(x) = x2
-
f(x) = 3x - 2
-
f(x) = |x|
-
g(x) = 2x + 1
-
h(x) = x/2 - 1
-
j(x) = √x
-
k(x) = (x + 2)/(x - 2)
-
l(x) = 3√x
-
m(x) = 5 - x
For every function:
1. Figure out if the function is one-to-one.
2. Graph the function and its inverse.
3. Figure out the inverse of the function algebraically.
4. Indicate the domain and range of every function and its inverse.
5. Use the inverse to solve for x in each calculation.
Grade Potential Can Help You Master You Functions
If you are having problems using one-to-one functions or similar topics, Grade Potential can put you in contact with a private teacher who can help. Our San Antonio math tutors are experienced educators who help students just like you improve their mastery of these concepts.
With Grade Potential, you can learn at your individual pace from the comfort of your own home. Schedule a meeting with Grade Potential today by calling (210) 879-9877 to learn more about our tutoring services. One of our team members will contact you to better inquire about your requirements to find the best teacher for you!